Astrasum is an independent research lab exploring better ways of evolving the human species.

Proactively Evolve through Darwinian Cycles

In 1859, Charles Darwin sent shock waves through Christian Europe with his idea that we might have descended from apes.

His On the Origin of Species introduced to the world the infamous theory of evolution. The theory, though ferociously debated for decades, has won scientific consensus as the most convincing theory that explains how life evolves and how we came to become humans.

According to his theory, we are alive today as humans because our ancestors, which went back as early as apes, survived changing environments with mutated genes as planet earth cycled on in the passage of time.

Some may ask, “If we are all descended from apes, then why are there still apes? Aren’t our ancestors all supposed to be dead already?”

Well, the apes we see today are really just our very distant relatives. And they are still apes because their ancestors never left the jungle, but ours did.

We look so different now as two different species because millions of years ago, some of the apes left the jungle. With such drastic change of the environment, survival became impossible for some, and only those with new genetic traits that happened to fit the natural demand of the new environment did survive.

What does that mean? It means evolution through natural selection is really just about the fitness or compatibility between new genetic traits and new environments.

Simply put, the genetic makeup of apes is highly compatible with the jungle environment. That is, it works if you live in the jungle, and so it survives and reproduces without having to change much.

And again, for those who inadvertently left the jungle, the same genetic makeup was no longer as compatible to the new environment, and so survival and reproduction only took place in those who have genetic mutations that happened to fit the new surroundings.

And therefore, evolution is never quite about the best genes in the absolute sense, nor is natural selection a one-sided business. Evolution is a mechanism in which genes mutate in each reproductive cycle, so that in times of drastic change in the environment, those genes that fit the changing environment the most would be ‘selected by nature’ to survive and then replicate in the next reproductive cycle.

It’s not about you or the environment. It's about you and the environment.

In simple terms, evolution is a cycle of mutation → selection → replication → mutation…

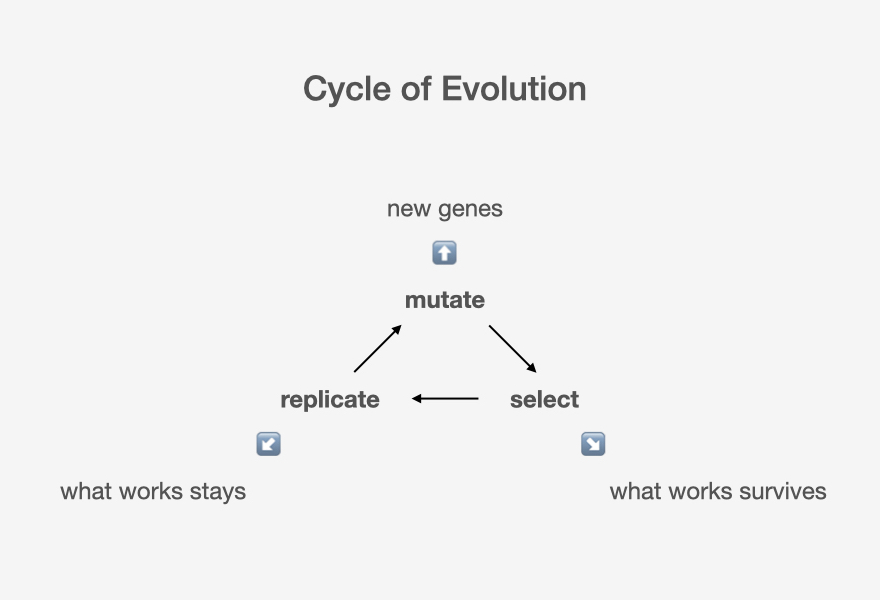
Through this cycle, life on earth spiralled from single-celled organisms to millions of different species, including one that’s dominated the planet and gone on to decode the secret behind this cycle of creation—Homo Sapiens.

Evolutionary cycle governs how life diversifies, survives, and reproduces. And if you consider the scientific method carefully, the cycle of knowledge creation seems to have a very similar shape as well.

It first takes on a wide array of hypotheses (mutation), and as opposed to indulging in conformation bias—finding clues to prove something right while ignoring the glaring signs that prove it wrong—the scientific method is about proving these hypotheses wrong, or falsifying them (selection), so that the surviving hypotheses become scientific theories, which would then be taught in schools and applied by scientists and engineers all over the world (replication).

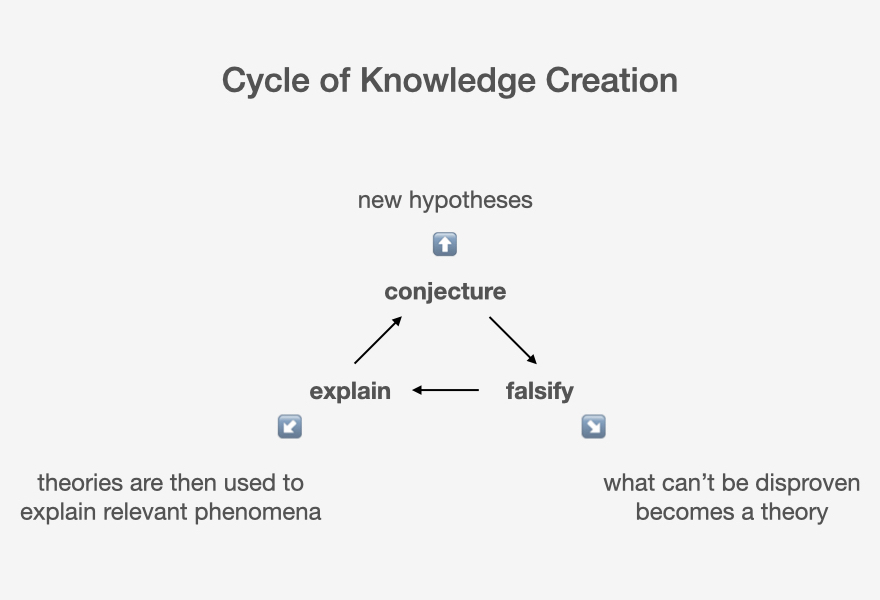
Of course, the cycle doesn't stop once a hypothesis gains the status of a theory. Scientific theories that survived decades or even centuries would often find themselves ‘unfit’ upon the new observation of phenomena previously unobserved, such as the advent of microscopes, which would then warrant new conjectures.

For instance, Einstein’s theory of planetary motion effectively succeeded Newton’s after over two centuries.

Interestingly, the cycle of scientific discovery—or knowledge creation—only started to become mainstream during the Enlightenment. From then on, humanity embarked on a high-speed train that’s been accelerating exponentially.

Is it a coincidence that the evolutionary cycle and the scientific cycle are ever so strikingly similar, not just in their capacity to facilitate creation, but also in the core elements that make up the cycle?

I think not.

Darwinian cycles as such—cycles that possess similar attributes to the evolutionary cycle—are more prevalent and creational than one might think.

As conscious human beings, we behave out of the cycle of feeling → thinking → acting → feeling...

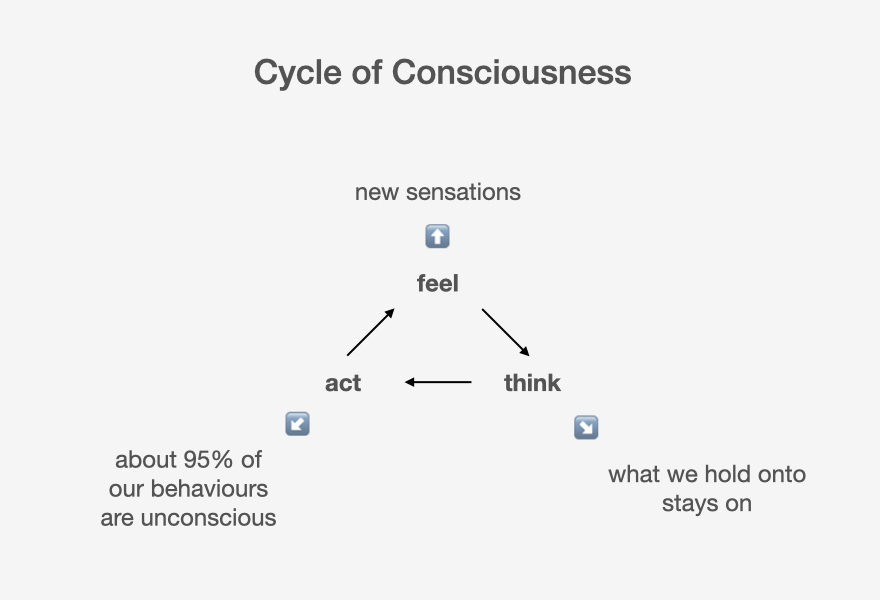
Because we weren't born with conscious behavioural habits, the younger we are, the more active this cycle typically is. And as we age, our brain adapts to most sensations and knows how to act, or react for that matter, upon feeling angry or happy or anxious. That is not to say that we cannot actively rewire our Darwinian cycle of consciousness as adults.

If we liken the sensations we feel as we sail through our daily experience to genetic traits, and our thinking mind as the habitat, then we may find that while we can't do much about what we feel, we are, in fact, very much in charge of the habitat—the mind.

Remeber evolution is about the compatibility between the genes and the environment? The good news is, the ability to transform our environment is unique to human beings. Within thousands of years, our species have managed to actively adapt to all kinds of habitats on earth and thereby spread ourselves all over the world

So here is a question: if we are ever so capable of changing our external environment, then are we really so powerless when it comes to our transforming our inner world?

Naturally, Darwinian cycles can also be found and applied in how we acquire skills:

How we cultivate relationships:

How we innovate:

And of course, these examples are just the tip of the iceberg. It's also worth noting that not every cyle that runs our life and work is a Darwinian cycle. More often than not, we are stuck in many problematic cycles.

What kinds of problematic cycles are out there?

Darwinian cycles can be short-circuited when there’s no mutation or selection or replication. In life, we can find ourselves helplessly stuck in short-circuited cycles, too.

For instance, we may come up with all kinds of interesting ideas at work, but when there’s no selection mechanism to filter these ideas, good ideas don't get to stand out and be brought to life.

Incomplete cycles can’t go on, so that’s when things really stop working and death, metaphorically or not, is imminent.

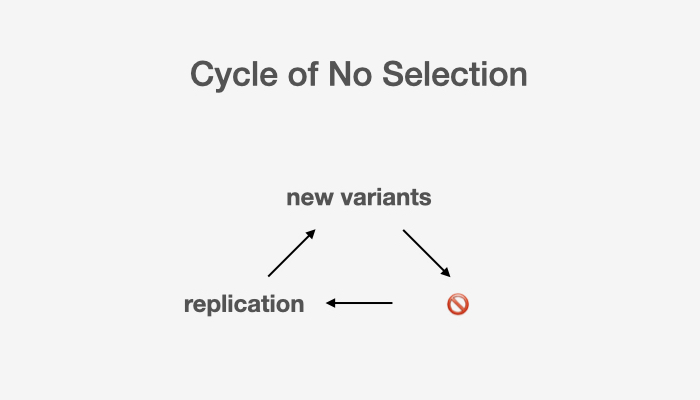
For startups especially, a good idea might be naturally selected out of all the brilliance of the founders, but if marketing and sales fall short in the replication process, a terrific idea could still be dead on arrival.

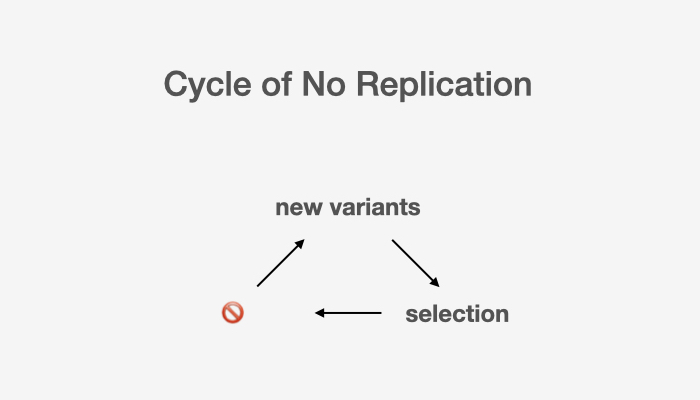
And it is rather obvious that any institutions or organisations that actively stifle new ideas, however contrarian they might first appear, are bound for eventual death.

Short-circuited cycles are the ones that are incomplete, but complete ones can still be useless. Useless cycles are the ones that do no harm but do no good, either. That may be how a lot of people feel when they are in school.

In most education systems around the world, we stuff our heads with all kinds of information and knowledge, yet the selection process is defined by what’s going to show up on the tests, not what’s going to be applied usefully in the real world.

It's good to be exposed to a variety of different fields of knowledge, but only if we absorb such new knowledge with a selection mechanism that's in touch with reality.

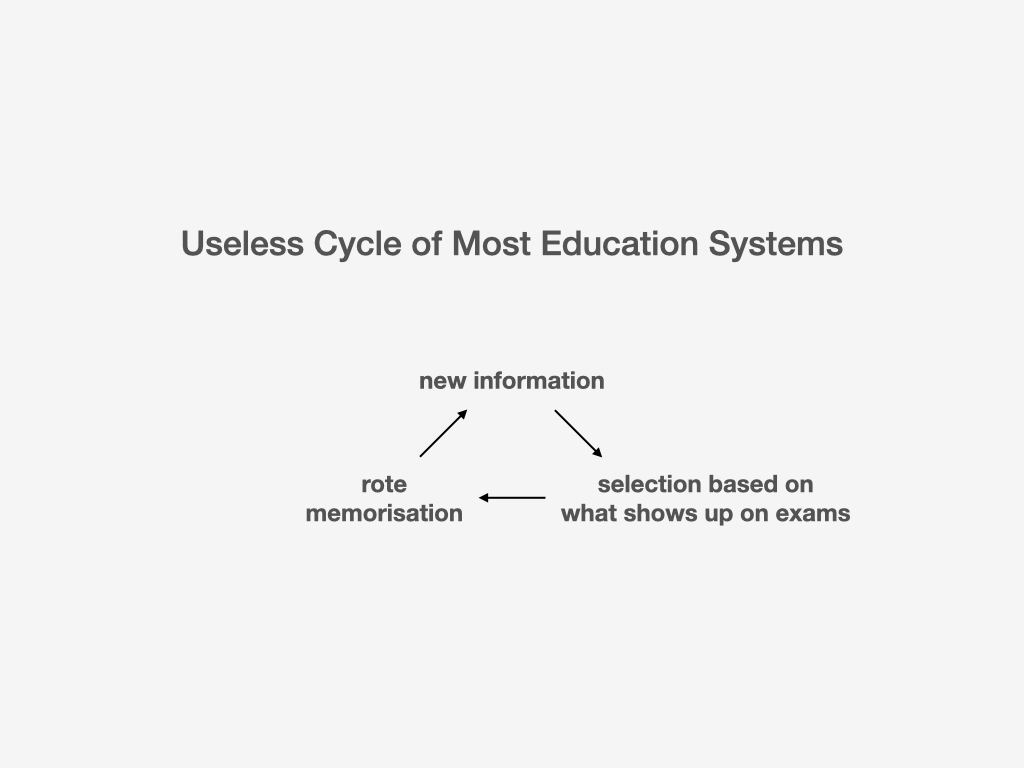
Useless cycles might seem harmless on the surface, but they could very much suck all the life and energy out of you.

For those who have been or are still stuck in such useless cycles, protect your curiosity and imagination at all cost.

The best analogy for a vicious cycle is cancer. That’s when there’s no new variants, no selection, and just reproduction. Short-circuited cycles left unattended could easily turn into vicious cycles.

Depression, for instance, often has its onset as one slowly descends into a vicious cycle. And in most cases, it is not until you lift yourself out of this cycle and settle into a Darwinian cycle of mental well-being—with the help of psychiatrists, therapists, the people you love, and above all, yourself—that you have a chance at healing.

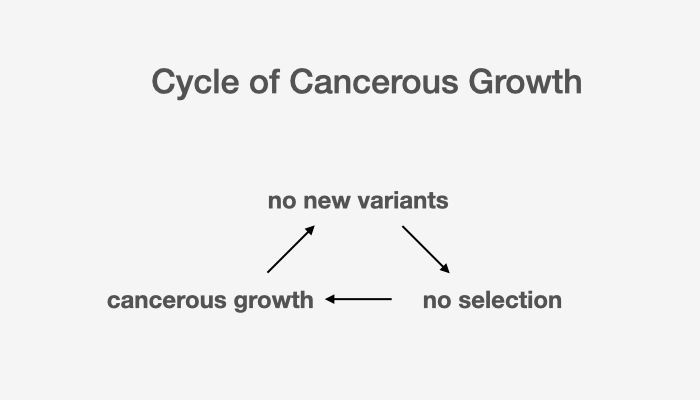
Doing nothing is often best practised when a Darwinian cycle is running just fine, but when you find yourself hopelessly stuck in a vicious cycle, doing nothing only makes things worse.

The most obvious example of all is if you find your health uncontrollably deteriorating, please go see a doctor immediately.

Astrasum got started in 2018 in a quest for exploring the future of learning, as the current system is failing to catch up to our ever changing world. For the most part, it was hundreds of unfruitful hypotheses and failed experiments.

Along this tumultuous journey, we’ve done many projects, all of which though could be put to good use individually, but hardly manifest our defining quest for a future we envision.

It took us a long time to get into a Darwinian cycle of discovery and innovation, which wasn’t surprisingly since we barely even knew what sort of cycles we were stuck in. Yet it is with this discovery that we realise that to learn means to evolve.

The future of learning is empowering every invidual and organisation to not passively, but proactively evolve through Darwinian cycles. Having gone through years of research and experiment by trial and error, we are both optimistic and confident that this can be made possible through community and technology.

On that note, please stay tuned for our latest research and projects!